Optimal Binary Search Trees

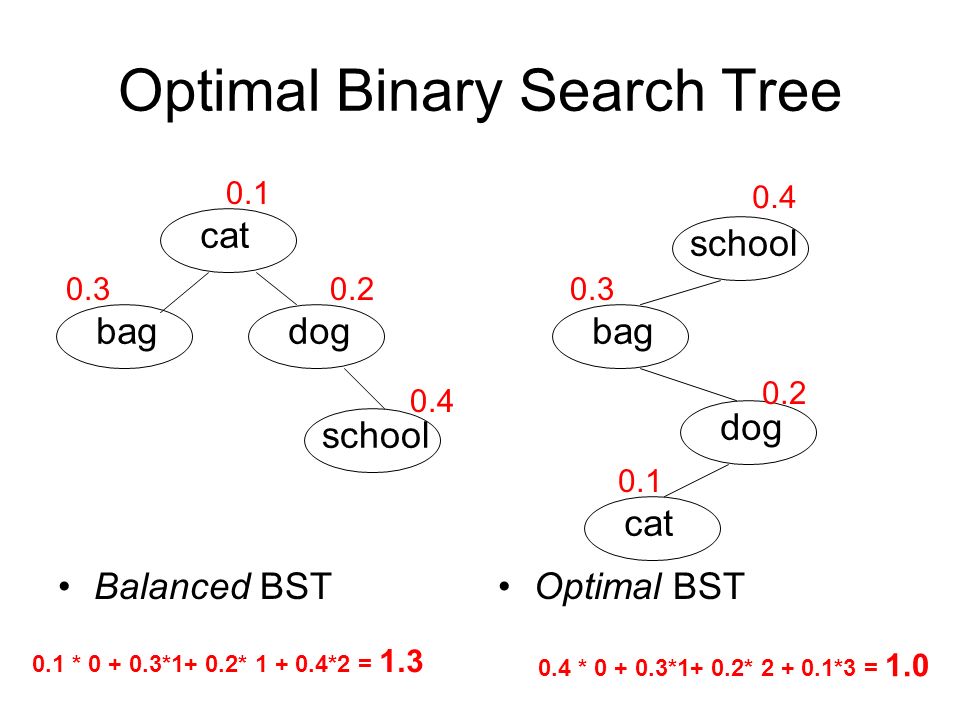
In this problem given a set of keys and their access frequencies, we have to construct a BST such that the least overall access time is achieved. For example suppose we have two keys [10,15] with frequencies as [10,30]. There can be two BSTs with one 10 as the root and the second with 15.

If we consider the first tree with 10 as the root then the overall cost = 10 * 1 + 30 * 2 = 70

If we consider the second tree with 20 as the root then overall cost = 10 * 2 + 30 * 1 = 50

Hence the structure of the tree affects the retrieval performance.

Dynamic Programming Approach

The naive approach for solving this problem is to create all the possible trees and calculate their costs. Then select the tree with the minimum cost. This program will have a factorial time complexity and the same sub-problems will be recomputed. Hence we attempt to solve this program using dynamic programming.

In this approach we create a two dimensional array (cost[n][n]) to store the solutions of subproblems; cost[i][j] specifies the minimum cost of the binary search tree considering the keys i to j. We first calculate the cost considering 2 keys, then 3 keys and so on until we cover all the keys. Which means we calculate c[1,2] i.e. the minimum cost considering keys 1 and 2, then c[2,3] and so on.

We can use the following formula to calculate c[i,j] where k goes from i to j.

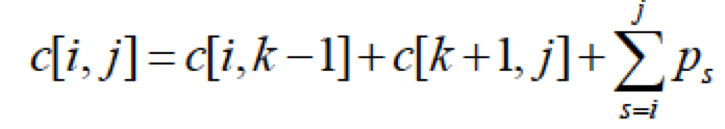
We store the minimum cost for c[i,j].

Parallelize Solution

We can easily parallelize this solution using Threading. The cost of constructing binary search trees with k keys can be calculated in parallel. For calculating the cost of a BST with k keys the cost of BSTs with k-1 keys is required. Hence there is no data dependence. Which means the cost of BSTs considering 2 keys can be calculated in parallel, then 3 keys can be calculated and so on. A graphical representation of the steps performed in parallel can be seen below.

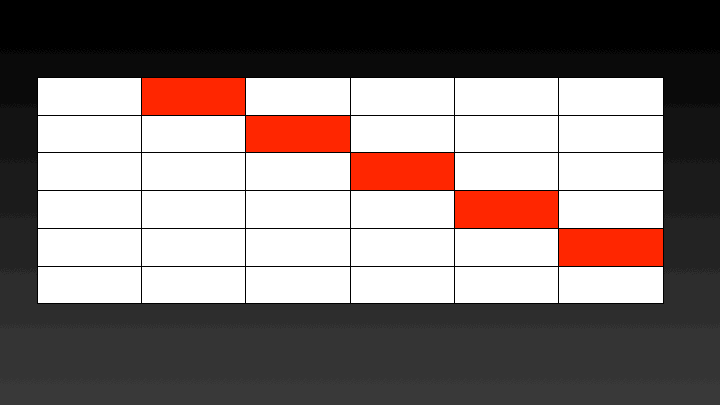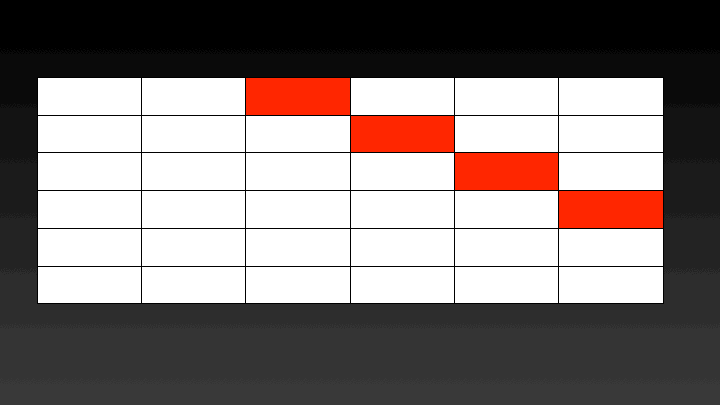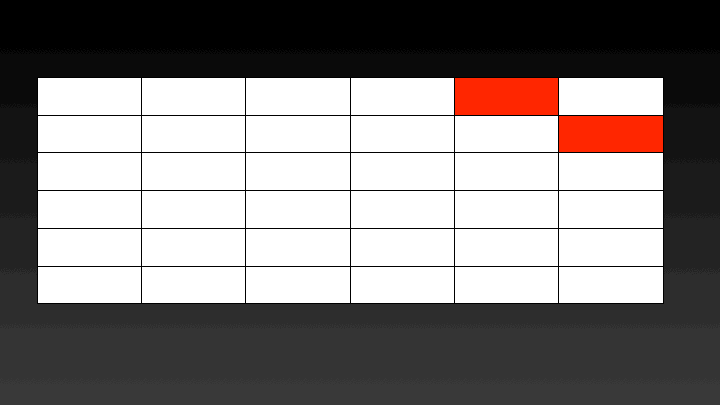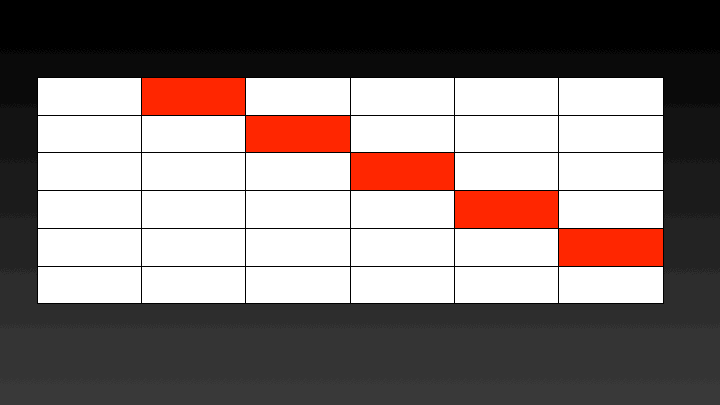
The catch is that all the threads should have completed calculating the cost of BSTs with k keys before moving to calculating the cost of BSTs with k+1 keys. To ensure this step this implementation uses a Barrier, which will let each thread go ahead once all the threads have reached it.

Case 1: N==P In this case, we have processors equal to the number of nodes. For this case, my approach will generate P threads and each thread will work on one row of the matrix.

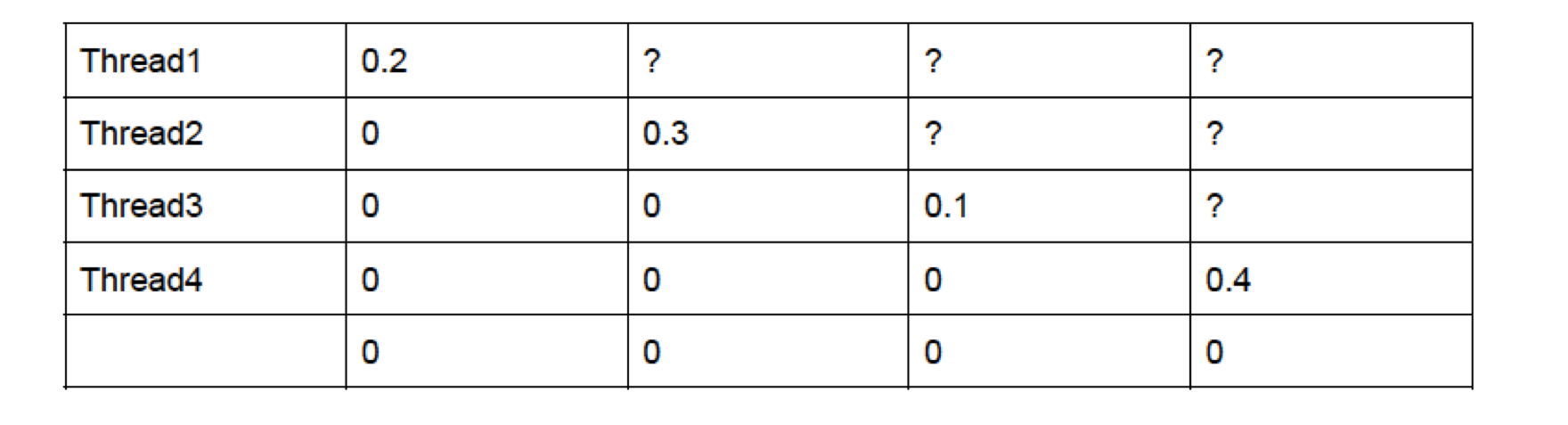The thread which works on the first row will take the maximum time since it needs to do the maximum number of computations. For n=4 it needs to compute the trees of size 2,3,4. For n=5 it needs to compute trees of size 2,3,4,5. Hence the complexity of the first thread will be O( n2 ). When performed serially the complexity is O( n3 ). In both cases, I am storing the sum of probabilities in an array and taking constant time to calculate the sum.

Case 2:N»P In this case, each thread will compute the values for N/P rows. Hence the time complexity for this program will be O( n3/ P ). Since we will have P threads running at a particular time. Speedup = Ts/Tp = n3 * P / n3 = P

Results

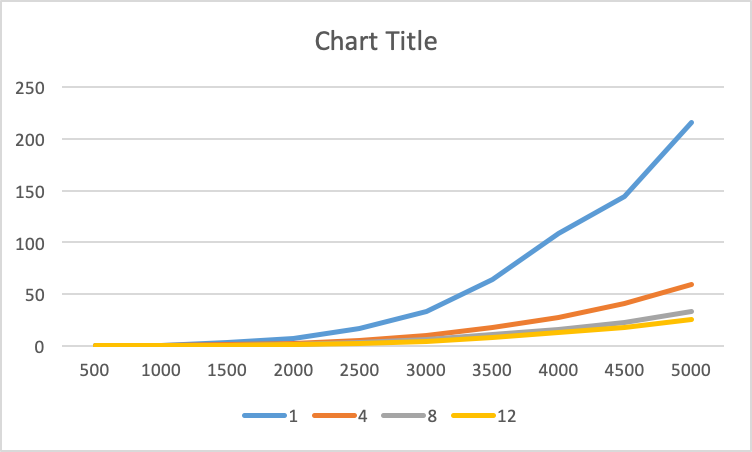
number of keys v/s Time in seconds; colors specify the number of threads

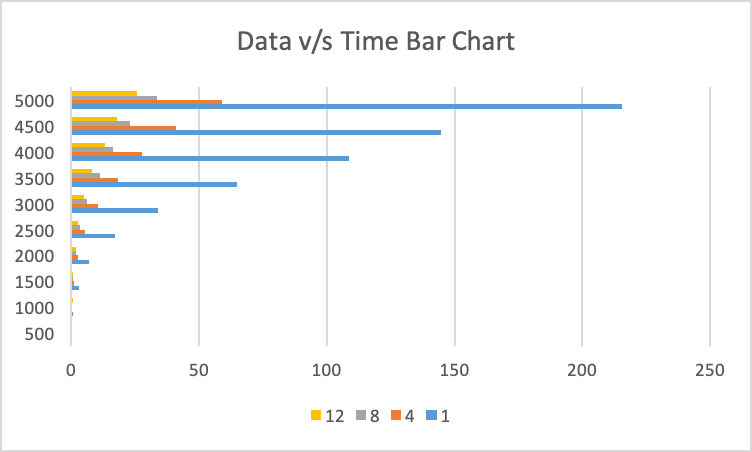
Bar chart of the same data

Running the Program

Given the number of keys the program will randomly generate the frequencies for these keys and generate the cost matrix

To run parallel_obst

javac parallel_obst.java,

java parallel_obst <number of keys> <number of threads>

example

java parallel_obst 5000 12

5000 - keys, 12- threads

This program requires serial_obst.java as well since after running it in parallel it will run it in serial. The program will calculate the cost in parallel and then calculate the cost in serial on the same frequencies To run serial_obst.java

javac serial_obst.java

java serial_obst <number of keys>

serial_obst will only print the total cost.