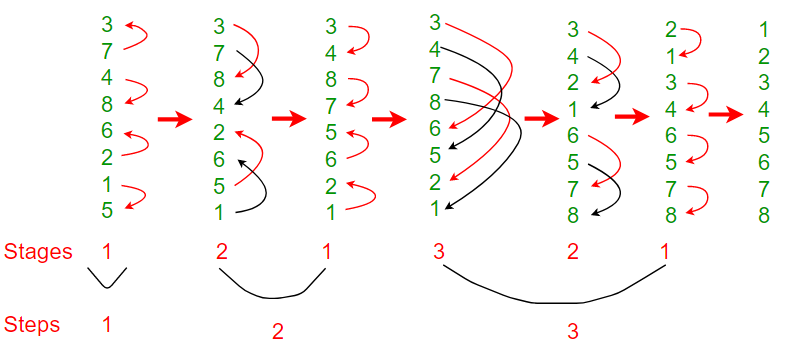
Bitonic Sort
Before looking at Bitonic sort let us look at the comparator circuits which form the basics of bitonic sort.

In the increasing comparator circuit (denoted by +) we provide two numbers. In the upper line we get the minimum of the two numbers as output while in the lower line we get the maximum number as output.
The decreasing comparator circuit (denoted by -) provides the reverse output. The upper line gets the maximum while the lower line gets the minimum value.
A bitonic sequence is one which is increasing and then decreasing for example 2,4,6,8,10,9,7,5,3,1 is a bitonic sequence. Now given a bitonic sequence it can be easily converted into a sorted sequence using the increasing comparator circuit.
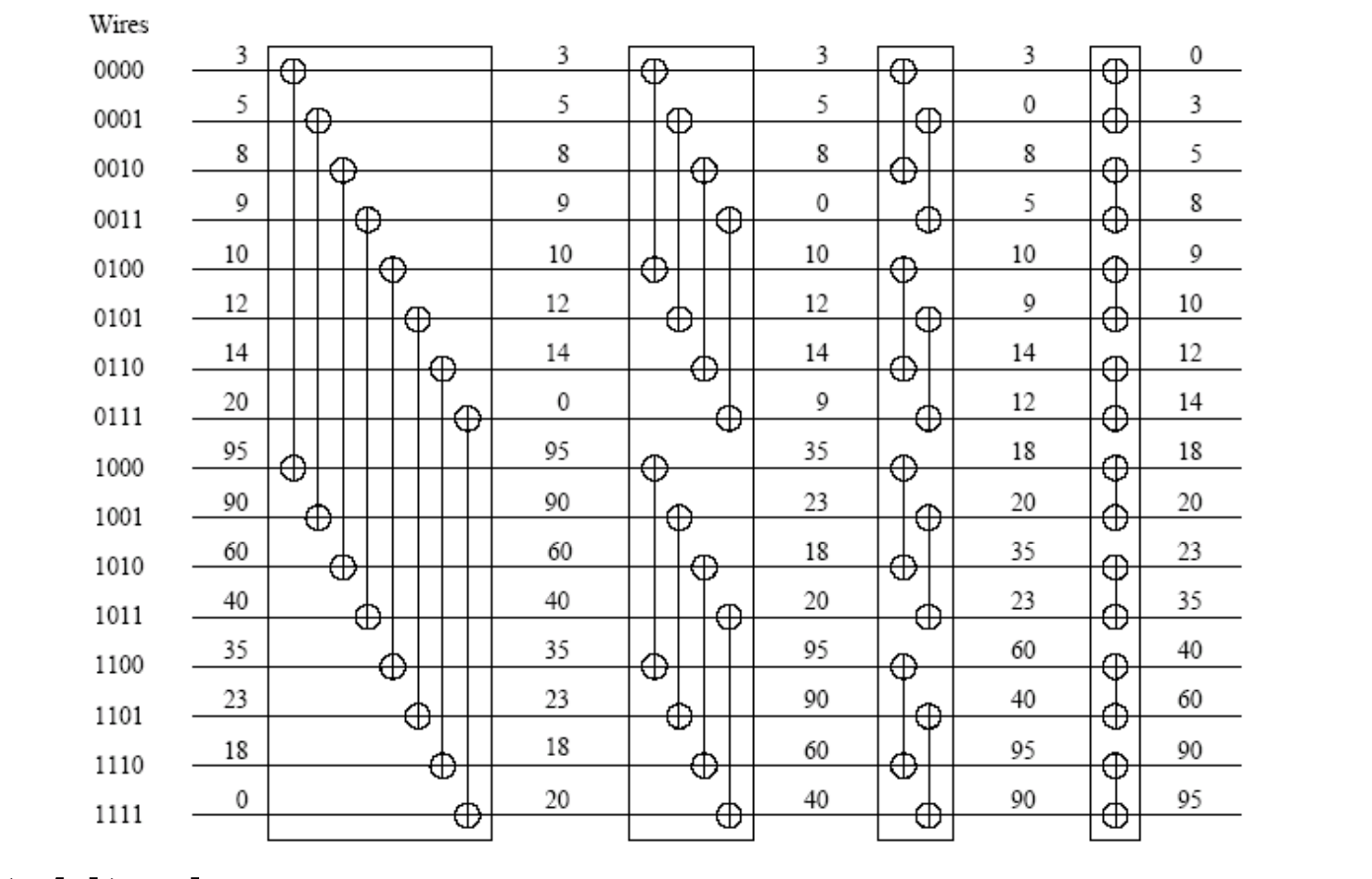
Now to convert a given sequence to bitonic we need the increasing as well as the decreasing comparator circuits.
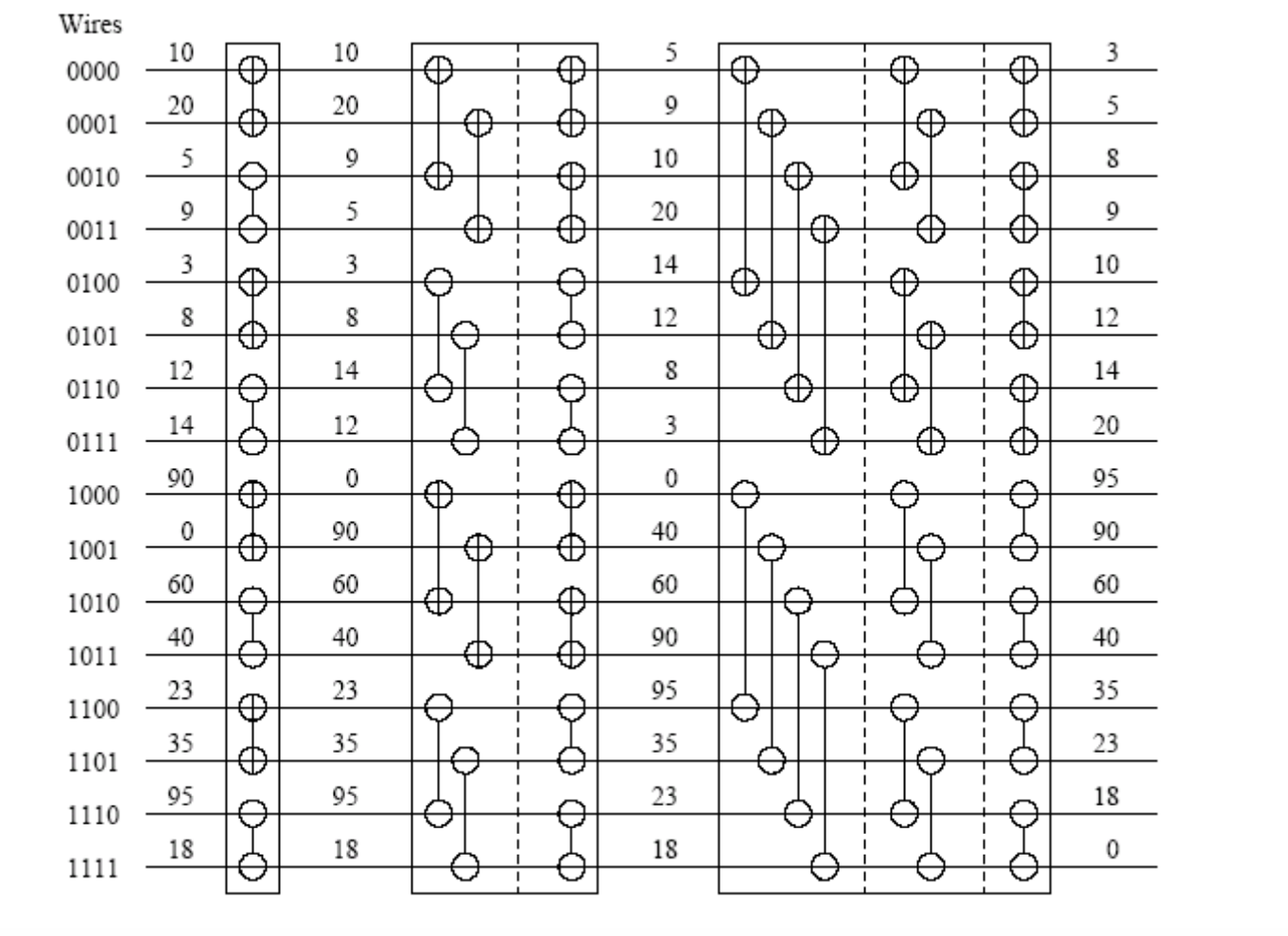
Now we can easily combine the two to get a sorted array
Image reference: https://wiki.rice.edu/confluence/download/attachments/4435861/comp322-s12-lec28-slides-JMC.pdf
Implementation
Bitonic sort is implemented using Message Passing Interface(MPI) in C.
The first step is generating a bitonic sequence.
If we closely look at the algorithm generating the bitonic sequence then we can find the pattern. In the first step each process compares with another process that differs at the first bit. In the second step with the process that differs at the second step and so on. This continues until the process number reaches log(p) and then we move back in.
Initially all the elements are distributed across the processes using scatter. Then to convert it into a bitonic sequence each process will calculate two things:
- Index of the next element
- It is a positive comparator circuit or a negative comparator circuit
Now there can be three scenarios:
- the next element is present on the same process
- the next element is present on a process with rank less than the current process
- the next element is present on a process with rank greater than the current process.
No communication is required for the first scenario, but data needs to be sent across processors for the second and third scenarios. The logic for data transfer is first process with the lower rank will send data and then the process with higher rank will send data. Blocking send and receive calls are used for data transfer. Finally the entire array is assembled at the process with rank 0 using the gather operation.
Results
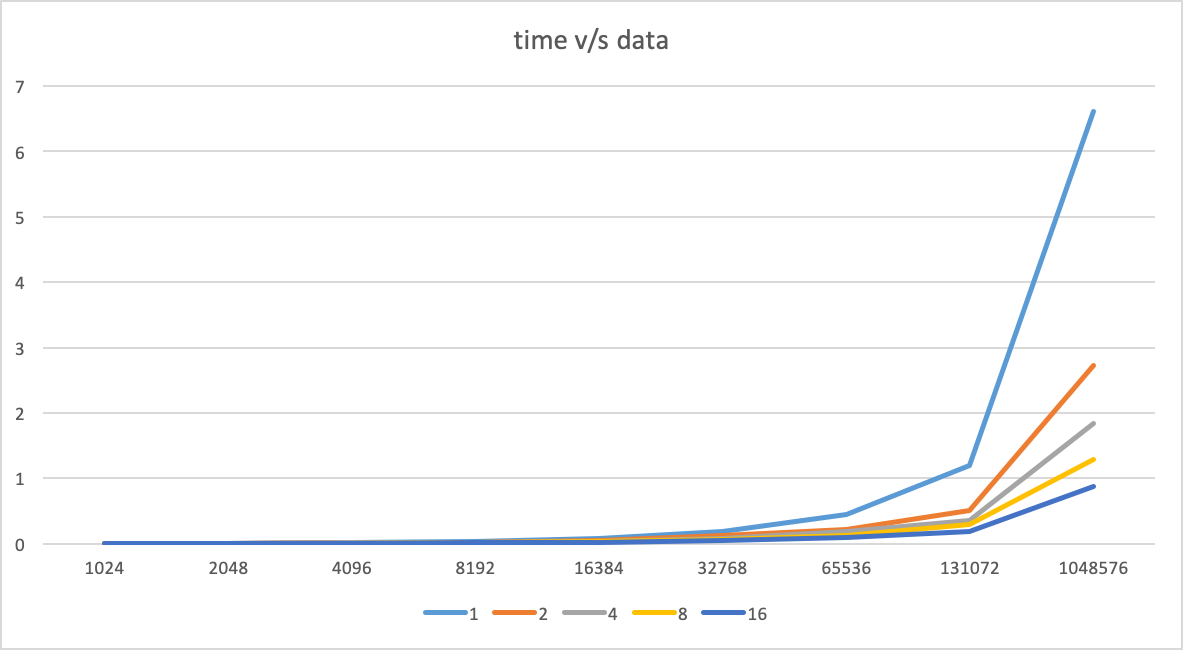
time v/s number of data elements; colors represent the number of processes
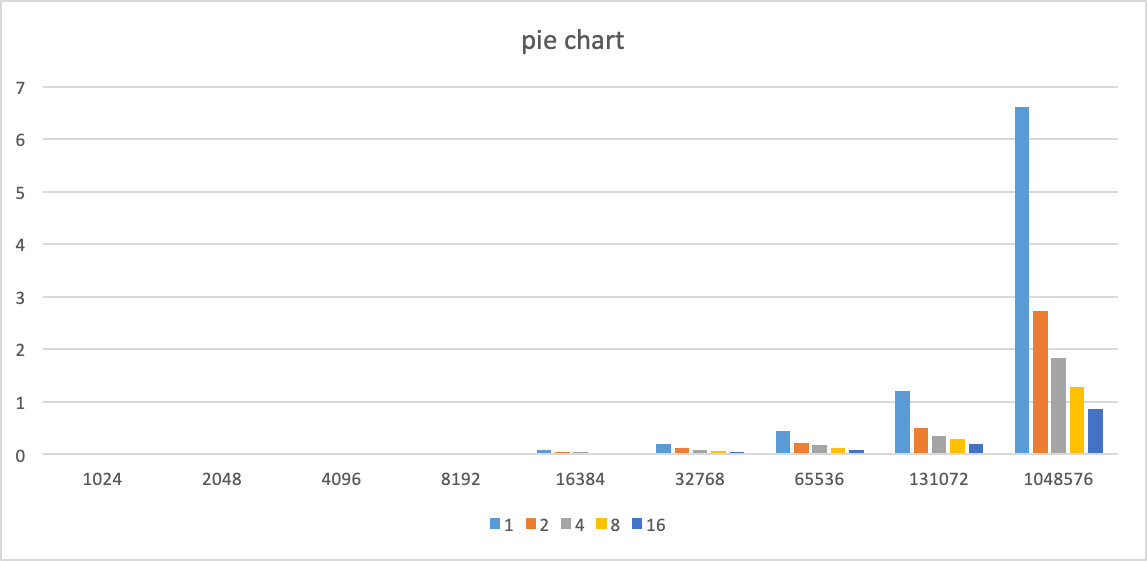
bar chart of time v/s number of data elements; colors represent the number of processes
Running the Program
Prerequisites MPI for C should be configured in the path
To compile the program
mpicc -o bitonic bitonic.c
Some machines give error for the math library so compile using
mpicc -o bitonic bitonic.c -lm
To run the program
mpirun -np <number of processes> ./bitonic <size of data> <1 or 2>
where <number of processes> is the number of processes to be created
<size of data> is the size of the array to be generated
<1 or 2> if 1 then the process will print the sorted array, if 2 will not print Both the number of processes and the size of data should be a power of 2 else the program will fail
e.g.
mpirun -np 16 ./bitonic 1048576 2
mpirun -np 8 ./bitonic 1024 2