Subgraph matching

Subgraph matching or subgraph isomorphism is an NP-complete problem, in which we have a target graph and a query graph. The goal is to to find all the occurrences of the query graph in the target graph.

Dataset

The dataset used for this project was the provided in ICPR2014 Contest on Graph Matching Algorithms for Pattern Search in Biological Databases. The query graphs are molecules while the target graphs are protein and backbone structures.

Algorithm

The basic algorithm is the famous backtracking algorithm published by Jeffrey Ullman in the famous paper. In this project some optimizations are implemented to reduce the search space which significantly reduces the run time.

Step 1: Local Candidate Reduction

In the first step we generate profiles are generated for each vertex in the query graph. Profile of a vertex is the prospective vertices in the target graph which might match the vertex in the query graph. In this case the matching vertex are those which have the same elements and the same number of edges.

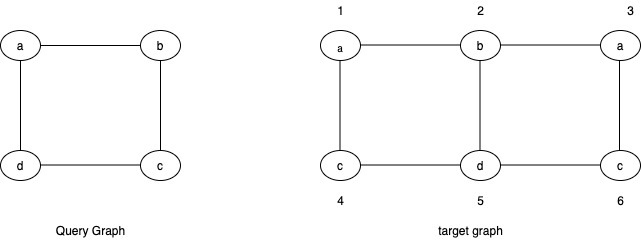
In this example for the query graph:

profile(a) = {1,3}

profile(b) = {2}

profile(c) = {4,6}

profile(d) = {5}

Step 2: Processing order

The next step is deciding the order in which the search should start. An optimal processing order will prune certain possibilities thus reducing the search space. The processing order is computed as per GraphQL. The idea is to compute a cost estimation of all the nodes. The reason for this is we can prune vertices with more connections earlier than the vertices with less connections.

Step 3: Early Stopping

While searching for matching vertices we can perform 1-look ahead and 2-look ahead as specified by the VF2 rules. The motivation behind this is even if two vertices match we can look at its neighbours and the neighbours of its neighbours, before matching.

Technology

The target as well as the query graph are stored in a Neo4J database and accessed using Cypher. These algorithms are implemented in Java.